DPの話
この記事は Competitive Programming Advent Calendar のために作成されました。
「DP (Dynamic Programminng: 動的計画法) がよく分からない」というつぶやきをよく目にします。何から何まで分からないというわけではないけど、
- 「こういうDPをすれば解けるよ」と説明されれば理解できるけど、一からそれを思い付けない
- メモ再帰だと書けるけどループだと書けない、またはその逆
とかいう。
この記事は、DPという技法をより深く理解する手助けをすることを目的として書かれています。これを読めばどんなDPの問題もさくさく解ける・・・ことはないと思いますが、あんまり悩まずに実装できるようになるぐらいの効果はあるんじゃないかなと思います。想定する読者層は、簡単なDPの問題をいくつか解いたことがある、TopCoderレーティング 1500 未満ぐらいの人としています。
DPとは何ぞや
ナップザック問題のアレとか巡回セールスマン問題のアレとかはDPに基づいたアルゴリズムです。では、DPとは一体何でしょう?この漠然とした質問にうまく答えられないというのが、ダイクストラとか線形計画法とかとは違う、DP特有の疑問なのではないでしょうか。
単刀直入にお答えしましょう。DPとは、DAG上の最短経路を求めることです。
コイン両替問題
のっけから大法螺を吹きましたが、これから詳しく説明していきます。以下の問題を例にとって考えましょう。
Problem Statement ちょうど n 円のお釣りを払おうとしています。使用できるコインは何種類かあり、i 番目のコインの額面は value[i] で与えられます。 どのコインを何枚使っても構いません。支払うコインの枚数の最小値を計算してください。(常に払えると仮定して構いません) Method signature int minChange(vector<int> value, int n) Examples 0) [1, 2, 4, 8, 16, 32] 63 Returns: 6 全てのコインを 1 枚ずつ使います。 1) [1, 5, 10, 50, 100, 500] 324 Returns: 9 日本の通貨体系です。 2) [1, 4, 9] 17 Returns: 3 4 + 4 + 9 = 17 とするのが最適です。
本質的に同じ問題として AOJ1167: Pollock's Conjecture がありますので、解きたい人はこちらでどうぞ。
この問題をDPで解くとすると、たとえば次のようなコードを書くことになるでしょう。
int minChange(vector<int> value, int n){ // dp[i] := i 円を払うお釣りの最小枚数 vector<int> dp(n + 1, inf); // n + 1 個の inf (十分大きな値) で初期化 dp[0] = 0; for(int i = 0; i <= n; ++i){ for(int j = 0; j < value.size(); ++j){ if(i - value[j] >= 0){ // 配列の範囲外チェック dp[i] = min(dp[i - value[j]] + 1, dp[i]); // i - value[j] 円払えるなら、それに value[j] 円を 1 枚足して i 円を払える } } } return dp[n]; }
このプログラムは、見方を変えれば DAG*1 上での最短経路を求めているのです。次のようなグラフを考えてみましょう。
n + 1 個のノード (0 ... n の番号を振る) を持ち、任意の j および ノード i について、 ノード i からノード i + value[j] へ有向辺が張られたグラフです。Example の最後のケースを描いてみましょう。

「17円を払う最小の枚数」というのは、「ノード 0 からノード 17 への最短経路」に一致しています (0 - 9 - 13 - 17)。よく見ると、17円だけでなく 1円から16円についても同様であることがわかるでしょう。このように、DPとは最短経路を求めることなのです。
最短経路だけじゃない
「じゃあ、フイボナッチ数を求めるこんなDPがあるけど」
int fib[N]; fib[0] = 1; fib[1] = 1; for(int i = 2; i < N; ++i) fib[i] = fib[i-1] + fib[i-2];
「これのどこが最短経路なんだね」という突っ込みがあるかと思います。
はい。DP == 最短経路 はちょっと言い過ぎました。このDPでは、最短経路ではなくパスの総数を求めていることになります。
フィボナッチ数の i 項目というのは、つまり 「ノード i - 1 から ノード i に、 ノード i - 2 から ノード i にエッジが張られたグラフにおける、ノード 0 からノード i へのパスの総数」に等しいのです。
もっと言いますと、「...の総数を求めなさい」というDPは、「...というDAGのパスの総数を求めなさい」と言い換えられます。同様に、「...の最小値を求めなさい」は「...というDAGの最短経路を求めなさい」に、最大値は最長経路に言い換えられるのです。
最長経路
最長経路の例も見てみましょう。LIS (Longest Increasing Subsequence) です。
Problem Statement 数列 a から 0 個以上の要素を取り除いて得られる数列を a の部分列 (subsequence) といいます。 与えられた数列の部分列で狭義単調増加 (全ての i < j に対して a[i] < a[j]) であるもののうち、最長のものを求めなさい。その長さを返しなさい。 Method signeture int LIS(vector<int> a) Examples 0) [3, 1, 4, 1, 5, 9, 2, 6] Returns: 4 このケースに対するLISは複数通りあります。[1, 4, 5, 6] などです。
これは、i < j に対して a[i] < a[j] であるような i, j 間に辺を張ったグラフの最長経路に等しいのでした。O(n^2) です。LIS の計算量は O(nlogn) まで落ちるのですが、今日は遅いDPで勘弁して下さい。
レッツ実装
世の中のDPの問題というのは、大抵次のように分類できます。
- 最短経路DP
- 最長経路DP
- 経路総数DP
- 確率DP (例: AOJ1277: Minimal Backgammon)
- 期待値DP (例: AOJ2236: スプリング・タイル)
- ゲームDP (例: AOJ1230: Nim)
これ以外にもあるかもしれません。
そろそろ実装の話に入りましょう。種類はいろいろありますが、やるべきことはどれも同じです。DAG上で最短路/最長路/パス総数etcを求めるには、トポロジカルソートして、トポロジカル順序の小さい順にノードの値を求めていきます。
ノード u[i] から v へ重み w[i] の辺が伸びているとき、v への最短経路長 minCost[v] は minCost[u[i]] + w[i] の最小値。そのまんまですね。グラフの頂点 v に対して、この minCost[v] の計算を、トポロジカル順序に沿って行なっていきます。トポロジカル順序に沿って計算しているのであれば、minCost[v] を求めるときには minCost[u[i]] は既に求まっているはずです。u[i] は v よりトポロジカルに前に来ていなければならないので、当然です。
一般のグラフの最短経路の場合、話はもう少し複雑でした。 こんなグラフがあったとき、
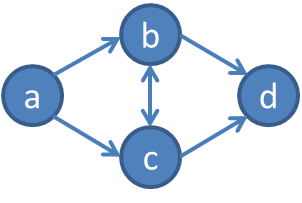
パス a - b - c - d も a - c - b - d もどちらも最短経路になりえる。minCost[b] が分かってから minCost[c] なのか、それとも minCost[c] を求めてそこから伸ばす形で minCost[b] なのか、はっきりしない。だから Dijkstra などという七面倒臭いことをしなければならなかったのです。幸いにもDAGはそうでない。トポロジカルソートできるのだから、b - c と c - b というパスが同時にありえるはずがないのです。a - b - c - d というトポロジカル順序が得られたら、b への最短経路に c が含まれることはない。c への最短経路は a か b から伸ばすしかない。だから頭から順番に計算できる。大変シンプルで良いことです。
トポロジカル順序
ですから、DPときたらまずはDFSを書いてトポロジカルソートしましょう!・・・はい、これは嘘ですね。DPの度にトポロジカルソートしているひとはあんまりいないと思います。現に上のコードもそんなことしてません。でも、さっきのコイン両替問題のグラフをもう一度見てみましょう。
トポロジカル順序など、トポロジカルソートするまでもなく明らかです。ノード 0, 1, 2, ..., n がそのまま答えになっています。それを踏まえてもう一度コードを見てみると、
int minChange(vector<int> value, int n){ // dp[i] := i 円を払うお釣りの最小枚数 vector<int> dp(n + 1, inf); // n + 1 個の inf (十分大きな値) で初期化 dp[0] = 0; for(int i = 0; i <= n; ++i){ // dp[i] をトポロジカル順序 (0, 1, 2, ..., n) の順に訪問して for(int j = 0; j < value.size(); ++j){ if(i - value[j] >= 0){ dp[i] = min(dp[i - value[j]] + 1, dp[i]); // 直前のノード dp[i - value[j]] から伸ばす } } } return dp[n]; }
ちゃんとトポロジカル順序を活用しています。
もうちょっと複雑な例を見てみましょう。巡回セールスマン問題です。
Problem Statement N 個のノードを持つグラフがあります。辺 i - j 間の重み (正の整数) が graph[i][j] で与えられます (辺がなければ graph[i][j] には十分大きな値が、graph[i][i] には 0 が与えられるものとします) 。 ノード 0 から出発して、すべての頂点を少なくとも一度訪問するコストの最小値を求めてください。最後にいる場所はどこでもいいです。 Method signature int travelingSalesmanProblem(vector< vector<int> > graph)
典型的な実装はこんな感じでしょうか。
int travelingSalesmanProblem(vector< vector<int> > graph){ const int n = graph.size(); // 頂点数 vector< vector<int> > dp(1<<n, vector<int>(n, inf)); // dp[1<<n][n] := dp[既に訪問したノードの集合][今いるノード] の最小コスト // 前処理としての Warshall-Floyd for(int k = 0; k < n; ++k) for(int i = 0; i < n; ++i) for(int j = 0; j < n; ++j) graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j]); dp[1][0] = 0; // ノード 0 だけを訪問している状態からはじめて for(int i = 0; i < (1<<n); ++i){ // 「既に訪問したノードの集合」の2進数表現の昇順かつ for(int j = 0; j < n; ++j){ // 「今いるノード」の昇順に訪問 if(i&(1<<j)){ // ノード j にいて、まだノード j を訪れてない状態 はありえないので弾く for(int k = 0; k < n; ++k){ // 次に行くノードに対するループ if(!(i&(1<<k))){ // ただし、既に訪問済みだったらやめる dp[i|(1<<k)][k] = min(dp[i|(1<<k)][k], dp[i][j] + graph[j][k]); // 更新! } } } } } // dp[全ノードを訪問した][どこでもいい] の最小値を返す return *min_element(dp[(1<<n)-1].begin(), dp[(1<<n)-1].end()); }
このDPでは、DAGのノードは (既に訪問したノードの集合 (の2進数表現), 今いるノード) のペアです。このペアの辞書式昇順でループを回して訪問しているのですが、DPが成り立つためには、この訪問順序がトポロジカル順序になっていなければなりません。本当にそうなっているでしょうか。いやそもそも、これってDAGでしたっけ。
ここで注目したいのが、更新式の i|(1<<k) です。2つ目の if で弾いていますので、次にセールスマンが巡回しようとするノード k は未訪問のノードです。つまり、更新の度に 巡回済みのノードの集合 i のサイズはちょうど 1 だけ増えるのです。このDPに対応するグラフ *2 に閉路があったならば、いくらでも更新することができてしまう。でも n 回も更新すれば巡回済みノード集合のサイズは n になって、それ以上更新できない。なので閉路はない。つまりDAGです。
で、k は未訪問であることから、 i|(1<<k) と i を整数として解釈したとき、i|(1<<k) のほうが大きいのも明らかです。 i は昇順にループしていますので、i|(1<<k) が i より先に訪問されてしまうことはない。なので、(既に訪問したノードの集合 (の2進数表現), 今いるノード) の昇順でループを回すと、ちゃんとトポロジカル順序になっています。
配るDP、貰うDP
注意深い人は、巡回セールスマン問題のコードとコイン両替問題のコードがちょっと違うのに気付いたと思います。巡回セールスマン問題の方では、トポロジカル順序で各ノードを訪問したときに、こんなことをしています。

コイン両替では前のノードを見て、コストの最小値をとっていました。しかし巡回セールスマン問題では、次のノードを見て min をとっています。トポロジカル順序を守ってさえいれば、こういうことをしても問題ありません。なぜなら、u[1] を訪れるときには u[1] よりも前のノードを既に訪れているはずだからです。min をとる順番は変わるものの、それによって最終的な計算結果が変わることはないのですね。
俗に、コイン両替みたいなのを「貰うDP」、巡回セールスマンみたいなのを「配るDP」と呼んだりするようです。どちらが優れている、ということはないと思います。書きやすい方で書きましょう。相互に書き換えるのも簡単ですし。
メモ再帰
「DAG最短経路を解くにはトポロジカル順序に沿ってループを回す」と言いましたが、よく知られた解法がもう一つ存在します。話の流れでこんなに後回しになってしまいましたが、全国1,000万のメモ再帰ファンの方々お待たせしました。メモ再帰です。
ループ解法がボトムアップ型なのに対し、こちらはトップダウン型と言えるかもしれません。貰うDPをそのまま再帰で書き表し、ついでにメモ化すればメモ再帰の完成です。
const int nil = -1; // 未計算であることを示す値 vector<int> memo; vector<int> value; int rec(int n){ if(n == 0) // 再帰の終了条件 return 0; if(memo[n] == nil){ // もし未計算だったら int result = inf; for(int i = 0; i < value.size(); ++i){ if(n - value[i] >= 0){ result = min(result, rec(n - value[i])); // 貰うDP } } memo[n] = result; // そしてメモ } // 計算済みなら即座に memo[n] の値が返される return memo[n]; } int minChange(vector<int> __value, int n){ memo = vector<int>(n + 1, nil); // メモの初期化 value = __value; // めんどいのでグローバルに持って行きます return rec(n); }
配るDPをメモ化でやってやれないことも無いと思うのですが、貰うDPのほうがずっと直感的です。貰うDPですから、メモ再帰も「トポロジカル順序に沿って埋めていく」戦略であることには変わりありません。
優劣比較
ループとメモ再帰、どちらが優れているでしょうか?両方とも広く使われていることからも分かるように、あまり大きな差があるわけではありません。特に、どちらも時間計算量 O(V + E)、空間計算量 O(V) と、計算量ではイーブンです。それぞれのメリットを強いて言うならば、
ループのメリット:
- コード長が短い (一般的な傾向として)
- 関数呼び出しのオーバーヘッドが無いので若干早い
- 深い再帰によるスタックオーバーフローのリスクがない
メモ再帰のメリット:
- トポロジカル順序を知らなくても直接適用できる
メモ再帰のメリットについては説明が必要でしょう。コイン両替問題のループ版では、0, 1, 2, ..., n がDAGのトポロジカル順序だと見切った上で、その順番で dp[i] についてループを回さなければなりませんでした。一方、メモ再帰ではそんなことお構いなしに、ただ貰う部分だけをコーディングしています。この「トポロジカル順序を意識しなくても、貰う部分だけを書けば動く」というメリットは、例えば範囲DP (配列 a に対して、その部分列 a[left .. right] に対する解 dp[left][right] を求めていくタイプのDP) のような、トポロジカル順序が見えづらい問題に対して大きな威力を発揮します。私は、そのような問題に対してはメモ再帰を、トポロジカル順序が明らかな問題に対してはループを使うことにしています。コード長が短いほうが好きなので。
ループではトポロジカル順序を意識する必要があって、メモ再帰では必要ない、それでいて計算量も同じというのは、不思議な感じがするかもしれません。これは、メモ再帰という操作がトポロジカルソートを暗に含んでいる為です。トポロジカルソートの典型的な実装はDFS、つまり再帰なのでした。この計算量も O(V + E) なので、定数倍としてメモ再帰の中に消えてしまうのです。
何にせよ、ループで解けてメモ再帰で解けない、あるいはその反対のような、時間/メモリ制限がタイトな問題はあんまり目にしません(そもそもそんな問題は作りにくいです)。両方使いこなせるようになった上で、書きやすい方を選ぶのがいいでしょう。
ところで、このループ版のみを DP と呼び、メモ再帰とDPを明確に区別している人もいるようです。一般的にどう捉えられているのかは知りませんが、個人的には区別する必要は感じません。解くべき問題をDAGの最短経路問題などに落とすこと、それをトポロジカル順序で埋めていくことで解くことにDPの本質があるのであって、どのように実装するかは瑣末であるように思うのです。あくまで私の独自解釈ですが。
普通に最短経路で解く
DAGの最短経路に落ちるのであれば、普通の最短経路アルゴリズム、つまりダイクストラでも解けて当然なはずでゲソ。コイン両替問題をダイクストラ・・・は面倒なのでBFSで解いてやろうじゃなイカ。
struct state{ int n, cost; }; int minChange(vector<int> value, int n){ vector<int> cost(n + 1, inf); queue<state> qu; for(qu.push((state){0, 0}); !qu.empty(); qu.pop()){ state st = qu.front(); if(cost[st.n] <= st.cost) continue; cost[st.n] = st.cost; for(int i = 0; i < value.size(); ++i){ if(st.n + value[i] <= n){ qu.push((state){ st.n + value[i], st.cost + 1 }); } } } return cost[n]; }
はいできた。この実装でも、トポロジカル順序を意識することなくコーディングできてしまっています。そういえばトポロジカルソートのもう一つの典型的な実装に、「入次数 0 のノード (とそこから伸びる辺) をひたすら取り除きまくる」というものがありましたが、あれはBFSするとさっくり実装できそうな感じでしたね。
最短経路以外
最短経路DPばっかり見てきて、最長経路や経路総数のDPがおろそかになっていました。が、最短経路が分かれば他のも簡単です。最短経路の更新式は、 min(minCost[ u[i] ] + w[i]) みたいな感じでした。足し算でコストを求めて、min をとる。
min を max に変えて、max(maxCost[ u[i] ] + w[i]) とすれば最長経路です。
確率DPはちょっと違って、 sum(probability[ u[i] ] * w[i]) といったところ。
経路総数は辺に重みが無いので sum(numPath[ u[i] ]) ですが、重みが無いのではなく、重み 1 固定と捉えると、 sum(numPath[ u[i] ] * w[i]) となって、確率DPと同じ式が出てきます。こうしてみると、色々あったはずのDPのパターンが大抵似たり寄ったりになってしまいました。
しかしながら、聡明な皆さんはさらなる共通した性質にお気付きのことでしょう。
- 最短経路は + と min
- 最長経路は + と max
- 確率DPは * と +
- 経路総数も * と +
min(x+z, y+z) = min(x, y) + z
まだわかりにくいので、min(foo, bar) のことを演算子で書くことにします。 foo▼bar で最小値を表すという記法を導入。書き直すと…
(x+z)▼(y+z) = (x▼y)+z
これは、分配法則です。記号が違うだけで、足し算と掛け算の分配法則 (x×z) + (y×z) =(x+y) × z と全く同じ形をしています。
「A地点からC地点の最短経路」という条件を文字通りに書くと (x+z)▼(y+z) つまり全部の可能な経路を作ってみて最小値を取る、 という計算になりますが、等式をみたら最適化のチャンス! min と + の分配法則によると、 (x▼y)+z つまり、代わりにまず落ち着いて途中までの最短路 (x▼y) を計算してから、 +z じっくり経路を延ばす、という計算法でも正しく答えが求まるわけです。 というのがダイクストラ法であり、ウォーシャル・フロイド法です。
さっきは、引き算の裏に結合法則の成り立つ足し算を見出して並列化をしました。 同じように、素直に書いたプログラムの裏に分配法則が潜んでいないか考えるのも重要です。 分配法則を使って高速な計算をするアルゴリズム導出法はあまりにも重要なので名前がついていて、 動的計画法 といいます。 競技プログラマーさんにはおなじみでしょう。
Derive Your Dreams - 計算のきまり
分!配!法!則!です!DPにまつわる各種演算は、+ と min であることや * と + であることが重要なのではなくて、分配法則が成り立つことが本質的に重要なのです。この記事は目からウロコでした。
DP問題の難しさ
さて、DP問題はDAG上の何かに帰着できる、という話をしてきました。コイン両替問題ではこのDAG構造は比較的見えやすいのですが、巡回セールスマン問題では、(既に通過した頂点の集合, 今いる頂点) という非自明なもの (経験を積んだ競技プログラマにとっては自明かもしれませんが) を持ち出さなければDAGに落とせませんでした。与えられた問題に対して、どんな状態空間を、どんなDAGを考えればよいのでしょうか。
これは非常に難しい質問です。逆に言えば、世の中のDPの問題は、まさにこの部分をプログラマに問うているのです。これに答えるためには、与えられた問題に対する深い洞察が必要です。愚直に状態空間を考えると爆発的に大きくなるけれども、問題特有の性質をうまく使うとそれが小さく抑えられる、というのがDP問題を解くときの非常に典型的なシナリオです。
まぁ、「それができたら苦労はせんわな」的な結論で終わるのもアレなので、それでもたまに役立つかもしれない DP tips をご紹介して終わりにしたいと思います。
状態空間以外を問うDP
DP問題というのは状態空間を考えさせるのが本質だと言いましたが、少数ながら例外もあります。AOJ1056: Ben Tohは 100,000 ^ 2 の状態空間が一瞬で見えるタイプのDPですが、アルゴリズム的な工夫によって空間を減らすのではなく、「ほとんどの状態はすごく小さいから 0 で近似できるよね」と言いながら計算をサボる問題でした。手前味噌ですが、私が作った問題の中でもお気に入りの一つです。同様の近似を要求する問題としては、AOJ2268: 乱択平衡二分探索木があります。hos' Xmas Contest 2010: Presentsも似たような話で、状態空間の多くが exactly 0 になることを解析的に示すことができて、計算をサボれる。
DAGにならない場合
問題を自然にグラフに落としたとき、ちょうどいいサイズのDAGになればいいのですが、DAGにならない場合もあります。その場合はどうしたらいいか。
最長経路や経路総数DPでは、そもそもそんなことが起きないことが多いです。というのも、DAGにならなければ最長経路や経路総数は無限大になってしまうので、「最大値を求めよ」という要求が無意味になってしまうからです。それでもしっかり問題として成立させている稀有な例がAOJ2307: Palindrome Gerenatorです。さすがwata先生。
確率DPや期待値DPでは、DAGに限りなく近いグラフが登場することがあります。DAGにring (両端の頂点が同じであるような辺) がくっついたようなものです。AOJ2236: スプリング・タイルとかですね。ring は簡単な式変形によって取り除けて、そのまま普通のDPになるのが定番です。DAGからは程遠いグラフになる期待値の問題がStrange Coupleです。この問題は期待値の関係式を書き下すと線形連立方程式に落ちるので、ガウスの消去法にでも放り込んでおしまいです。
最短経路が一番わかりやすくて、ダイクストラでもすればよろしい。AOJ1150: Cliff Climbingとか、いわゆる拡張ダイクストラとか呼ばれる類の問題です。また、計算量さえ許せば、次元を増やして強引にDAGに持ち込むことも出来ます。普通の (DAGに限らない) 最短経路問題をDPで解いてみましょう。
N 個のノードを持つグラフがあります。辺 i - j 間の重み (正の整数) が graph[i][j] で与えられます (辺がなければ graph[i][j] には十分大きな値が、graph[i][i] には 0 が与えられるものとします) 。 ノード 0 から出発して、ノード N - 1 に到達する最小コストを求めてください。 Method signature int shortestPath(vector< vector<int> > graph)
int shortestPath(vector< vector<int> > graph){ const int n = graph.size(); vector< vector<int> > dp(n, vector<int>(n, inf)); dp[0][0] = 0; for(int t = 0; t < n - 1; ++t){ for(int i = 0; i < n; ++i){ for(int j = 0; j < n; ++j){ dp[t+1][j] = min(dp[t+1][j], dp[t][i] + graph[i][j]); } } } int result = inf; for(int t = 0; t < n; ++t) result = min(result, dp[t][n-1]); return result; }
dp[t][i] := ちょうど t 回の移動でノード i に移動する最小コストを求めていくDPです。t からは t + 1 にしか移動しないので、これでちゃんとDAGになりました。頂点数 N のグラフで、最短経路の長さが N - 1 を越えることはないので、そこまで調べれば十分です。(result の線形探索も本当はいらないんですが、分かりやすさのために残しときます。) ダイクストラに比べて時間もメモリもバカ食いしてますが、こんなシンプルなのも乙なものでしょう。
ところで、 O(n^2) もメモリを食うのは贅沢です。これをケチって1次元にしてしまい、dp[t][i] が必要なときはいつでも dp'[i] を使うようにしてしまいましょう。これは元のプログラムとは違うものを計算していますが、それでも最終的に最短経路はしっかり求まってしまいます。というのも、こうすると dp'[i] は常に dp[t][i] 以下になるけれども、「任意回の移動でノード i に移動する最小コスト」を下回ることはないからです。こうやってメモリ O(n)、 時間 O(n^3) の最短経路DPが生まれました。このアルゴリズムには既に名前がついていて、Bellman-Ford といいます。
終わりに
「DPは特殊技能」という言葉が一昔前のICPCerの間で囁かれていたそうです。それだけDPには典型的な思考法が存在せず、そのアルゴリズムの設計は各人の経験知によるところが大きかったのでしょう。今でも一つのDPの問題やアルゴリズムを取り上げて解説した記事はいくらでもありますが、あらゆるDPアルゴリズムにあまねく共通する性質を掘り下げたものは多くありません。
この記事では、DPとDAGの関係性について着目して解説しました。結果として、ループやメモ再帰といった実装上の些細な問題で躓かないようになり、その問題特有の性質についてより深く考察できるようになることを目標としました。DPとDAGの関係性を大きく取り上げた記事を私は他に見たことがなく、このDPの解釈がどこまで通用するかはよく分からないというのが本音だったりします。RedCoderの方々はDPをどのように捉えているのでしょうか。いろんな人のブログを見る限り、DAGというのはそれほど外していないように思うのですが。
最後に、この記事は眠気の中で勢いで書かれました。大嘘こいてるかもしれません。特にソースコードはコンパイルすら通してないので、バグってたらごめんなさい。疑問質問はコメントにて受け付けます。
それでは、Happy Dynamic Programming!


